Structural Equation Modeling in IS Research - Understanding
the LISREL and PLS perspective
Wynne W. Chin
University of Houston
As in many other social science areas, the IS field has seen a substantial
increase in the number of submissions and publications using structural
equation modeling (SEM) techniques. This is likely due to the proliferation
of software packages to perform covariance-based (e.g., LISREL, EQS, AMOS,
SEPATH, RAMONA, MX, and CALIS) and component-based (e.g., PLS-PC, PLS-Graph)
analysis. The SEM approach is integrative in the sense that it combines
the perspective of two research traditions:
-
an econometric perspective focusing on prediction
and,
-
a psychometric emphasis that models concepts as
latent (unobserved) variables that are indirectly inferred from multiple
observed measures (alternately termed as indicators or manifest variables).
This resulting combination allows researchers to
perform path analytic modeling with latent variables (LVs). Specifically,
SEM provides the researcher with the flexibility to: (a) model relationships
among multiple predictor and criterion variables, (b) construct unobservable
LVs, (c) model errors in measurements for observed variables, and (d) statistically
test a priori substantive/theoretical and measurement assumptions against
empirical data (i.e., confirmatory analysis).
SEM involves generalizations and extensions of
earlier first-generation procedures. By applying certain constraints or
assumptions on an SEM analysis, a researcher can end up performing the
equivalent of techniques such as canonical correlation, multiple regression,
multiple discriminant analysis, analysis of variance or covariance, or
principle components analysis.
Naturally, along with the benefits comes the complexity. This virtual
discussion will cover various issues that often appear among researchers.
The primary focus will be on both the covariance based approach often equated
generically as a LISREL analysis and the Partial Least Squares approach.
Hopefully, we will not only cover matters generic to social scientists,
but also specific to the IS field. To guide the questions, we might look
at it from various frames.
One standard approach is to examine the stages in the traditional SEM
lifecycle. They are:
-
Model Specification,
-
Identification,
-
Estimation,
-
Testing Fit, and
-
Model Modification or Respecification.
Another approach is to examine common mistakes that are made. We can discuss
such issues as:
-
Critical Missing Information. Information that should be included
but are often left out from research articles thereby preventing other
researcher from reproducing the analysis and building a cumulative tradition.
-
Mismatch of questionnaire items and subsequent analysis. Survey
questions analyzed are often formative in nature or a composite
of formative and reflective measures. A LISREL analysis and use
of internal consistency measures such as Cronbach’s alpha would be incorrect.
-
Sole reliance of overall goodness of fit measures. Using only covariance
based goodness of fit measures as the primary arbiter of confirmation while
ignoring other important measures of model adequacy.
-
Analyzing second order factors without a purpose. Demonstrating
second order factor models without providing an underlying rationale for
its subsequent usage.
-
Lack of Empirical over-identification. Many empirical studies do
not perform a strong test of the model/latent variables.
-
Ignoring the statistical power of models.
-
Ignoring equivalent models.
-
Falling into an exploratory mode via initial exploratory factor
analysis or using information from the statistical package to modify initial
models for better fit.
-
Premature or inappropriate approach of analysis when either substantive
or theoretical knowledge is relatively new.
Finally, we can approach it from an applied perspective. Example
questions might include:
-
When should I consider using Partial Least Squares as opposed to LISREL?
-
More importantly - how does Partial Least Square differ from LISREL?
-
How does LISREL compare to path analysis using multiple regression?
-
Does it make sense to do an exploratory factor analysis prior to using
SEM?
-
How about a confirmatory factor analysis first?
-
What are the advantages to using SEM for multi-sample or cross-cultural
analysis?
To start off, we might consider the following model (Figure 1) as a basis
for discussion. The model is a simple two factor model where F1 is hypothesized
to affect F2. The data in the form of a correlation matrix is provided
in Table 1 for the four measures/indicators (x1,x2,y1,and y2) of their
respective factors.
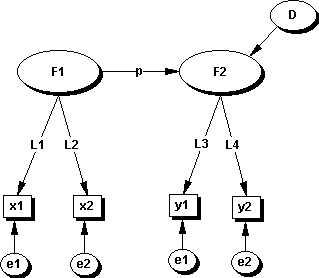
Figure 1. Two factor model with two indicator/measures for each factor.
| |
x1
|
x2
|
y1
|
y2
|
|
x1
|
1.00
|
|
|
|
|
x2
|
.087
|
1.00
|
|
|
|
y1
|
.140
|
.080
|
1.00
|
|
|
y2
|
.152
|
.143
|
.272
|
1.00
|
Table 1. Sample Data Set (n=1000).
All correlations, given the sample size, are
significant but quite low ranging from 0.087 to 0.272. If we use the theoretical
model as depicted in Figure 1, what would be the path estimate p
linking F1 and F2? The covariance based estimate using software such as
LISREL would result in a standardized estimate of p at 0.83 whereas the
PLS estimate was 0.22. The standardized loadings of a, b, c, d using the
covariance procedure were 0.33, 0.26, 0.46, and 0.59. The PLS estimates
resulted in loadings of 0.81, 0.66, 0.73, and 0.85 with corresponding weights
of 0.75, 0.60, 0.54, and 0.71. In the case of the covariance estimates,
the path estimate of 0.83 is much larger than the observed correlations
between the x and y variables where the highest is 0.152. In the case of
PLS, the estimate of 0.22 is much closer to the observed correlations.
Which estimate should we place confidence in?

