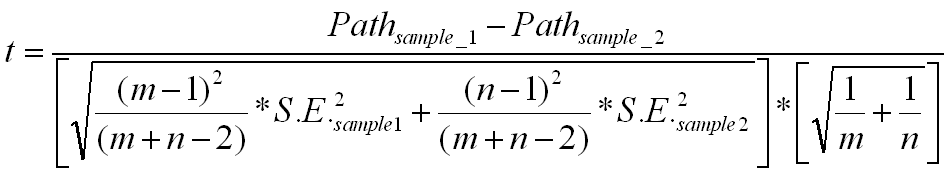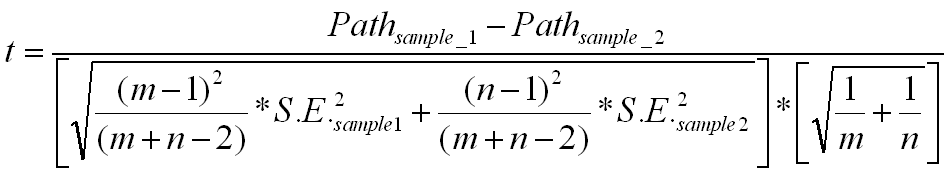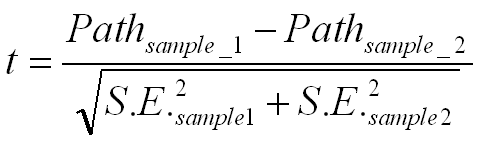Multi-Group analysis
with PLS updated 12/21/2004
-
I need some advice. I have a set of husband and wife response to the same
questionnaire in a cross-cultural context (i.e. Australian, Chinese, Malay)
and I am thinking about the possibilities.
-
Is it possible to treat the husband and wife data as indicators of the same
variable in PLSGRAPH? That is instead of combining them manually or
something else (e. g. difference scores) I could simply treat it as a part
of the outer model. What do you think?
Answer:
Indeed you could. If both the husband and wife answer the same questions (i.e.,
the same attitude object), you can treat them as reflective indicators of the
same underlying issue. Alternatively, you might even treat them as formative
indicators if you view them as capturing different perspectives of an issue. In
the case of reflective indicators, there is concern regarding the
non-independence of the two measures which may lead to a bias of higher
convergence (equivalent to a method effect). Under covariance based procedures,
you might model this impact by correlating the error terms for the two
indicators. Under PLS (not currently available in PLS-Graph), you could would
model a second component.
3. Could
I treat the cross-cultural aspect as a categorical variable in PLSGRAPH or must
I do multiple group analysis in LISREL?
Answer:
You can examine differences in structural across the cultural groupings. It's
not automated in PLS-Graph. So, you'd need to take the standard errors for the
structural paths provided by PLS-Graph in the re-sampling output and hand
calculate it.
The ideal approach would be to do it non-parametrically. I've always planned to
develop a permutation approach in PLS-Graph and it is currently under
development. This requires you to randomly
select cases from the combined multi-group set for each group. Then request the PLS-Graph software to run the samples and print out the results of the
re-sampling, sorting the data for each parameter for each population. This is
probably way beyond what is expected in current applied papers.
The other approach, which is the most expedient, is to treat the estimates of
the re-sampling in a parametric sense via t-tests. You make a parametric
assumption and take the standard errors for the structural paths provided by PLS-Graph
in the re-sampling output and hand calculate the t-test for the difference in
paths between groups.
Essentially, run bootstrap re-samplings for the various groups and treat the
standard error estimates from each re-sampling in a parametric sense via
t-tests.
You need to calculate the pooled estimator for the variance, which is
Sp =Square root of {[square of (m-1)/(m+n-2)]*square of SE for sample1 +
[square of (n-1)/(m+n-2)]*square of SE for sample2}
Then subtract the paths for the two samples. Take this difference and divide by
Sp* Square root of (1/m + 1/n)
The complete formula is as follows:
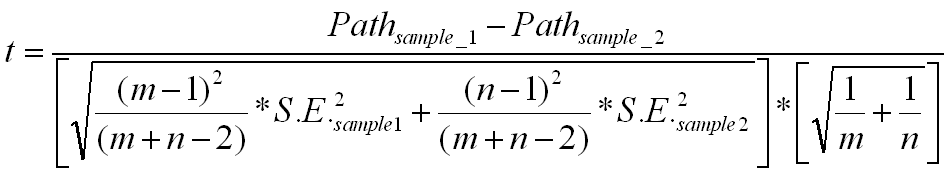
This would follow a t-distribution with m+n-2 degrees of freedom.
One caveat in this approach is that there is an assumption that the underlying
weights in the formation of constructs for each grouping are approximately
equivalent.
Overall, this approach works reasonably well if the two samples are not too
non normal and/or the two variances are not too different from one another. If
the variance for the two samples are assumed different, a Smith-Satterthwait
test can be applied.
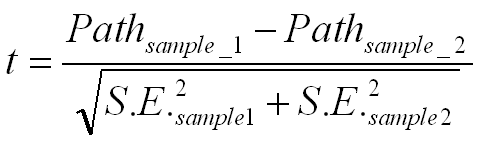
Unless the N's are large, we need to calculate the degrees of freedom as
follows:

The only difference between the first and second procedure is the assumption
of equal variances for the two populations. If the variances are equal,
the second procedure would be less efficient. But for large samples, both
procedures should yield similar results when the variances are equal.
Note: The formula may differ from standard texts contrasting regression
coefficients. The reason for the difference is the use of the bootstrapped
standard error. This standard error is already mean adjusted reflecting the
standard deviation of the sampling distribution as opposed to the sample or
population standard deviation. The formula in many books assume the latter and
goes on to adjust by the sample size. So, we need to correct for it by
multiplying the SE from the bootstrap by the square root of the sample as well.
In other words, (n-1)*square (SE from bootstrap) represents the variance of the
sample.