When you go through the formal model specification and the basic PLS estimation process, the requirements for sample size becomes reasonably clear for all three stages of the estimation process.  It has to do with the fact that either simple or multiple regressions is performed depending on the mode for each block of indicators and the inner weighting scheme. Due to the partial nature of the estimation procedure where only a portion of the model is involved at any one time, only the part that requires the largest multiple regression becomes important. And while stage 2 and 3 are equivalent in sample size requirements, stage 1 may not require as large a sample size contingent on which inner approximation is selected.

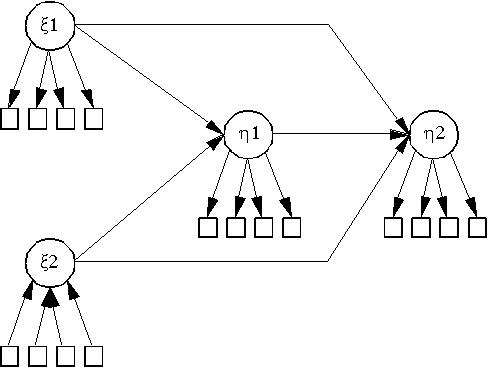
Overall, for adequate power at stages 2 and 3, you simply have to look at the model specification or equivalently the graphical model such as that depicted in Figure 1 and find the largest of two possibilities: 1) the block with the largest number of formative indicators (i.e., largest measurement equation) or 2) the dependent LV with the largest number of independent LVs impacting it (i.e., largest structural equation). If you use a regression heuristic of ten cases per predictor, the sample size requirement would be ten times either 1) or 2), whichever is the greater. For a more accurate assessment, you would specify the effect size for each regression analysis and look up the power tables provided by Cohen (1988) or Green’s (1991) approximation to these tables.

Using Figure 1 as an example, the only block with formative indicators consists of four indicators impacting x2. The dependent LV with the largest number of independent LVs impacting it is h2 with three paths going into it. Thus, the largest regression at any one time consists of four independent variables. Assuming a medium effect size as defined by Cohen (1988), you would need a minimum sample size of 84 to obtain a power of 0.80. With a large effect size, the sample requirement drops to 39.

For stage 1, the use of a path weighting scheme would result in the same sample requirements as necessary for stages 2 and 3. But with the use of a factor or centroid weighting scheme, only simple regressions between the LVs are performed in calculating the weights to be used for the inside approximation. In this situation, only the measurement model with formative indicators becomes the critical factor in sample size requirements. Had all latent variables been modeled as reflective (mode A), the use of either a factor or centroid weighting scheme would entail only a series of simple regressions during the entire stage 1 process resulting in a minimum sample size requirement of 53 and 24 for medium and large effect sizes.

In fact, the minimum sample size required to assess component loadings for reflective indicators is likely even smaller. Given that the standard requirement for loadings are normally set at 0.60 or above, the effect size of component loadings are larger than what is considered large in regression power analysis (i.e., f ²of 0.35, Cohen, 1988). For example, a 0.60 loading represents an f² effect size of 0.56 and requires a sample size of 15 to obtain a power of 0.80 for detection. This situation is demonstrated partly in a Monte Carlo study where sample sizes of 20 could not detect structural paths of 0.40, but easily detected loadings of 0.60 and 0.80.

More information about PLS and sample size can be obtained from the following paper:

Chin, W. W., and Newsted, P. R. (1999). Structural Equation Modeling analysis with Small Samples Using Partial Least Squares. In Rick Hoyle (Ed.),  Statistical Strategies for Small Sample Research, Sage Publications, pp. 307-341.